How we investigated Sweden’s Suspicion Machine

INTRODUTION

Over the past three years, Lighthouse Reports has investigated the use of machine learning risk-scoring algorithms in European welfare states. These systems are increasingly deployed across the continent and score millions of people. They make life-changing decisions about thousands of people, subjecting them to invasive investigations where small mistakes can leave welfare recipients without money to pay bills, food and rent. Despite the high stakes involved, governments are often reluctant to provide meaningful information about the systems. This makes it difficult to hold officials accountable when they are faulty and discriminatory.

In Sweden, the country’s Social Security Agency deploys machine learning at scale to score hundreds of thousands of welfare applicants and flag them for invasive investigations that can leave people without benefits they are entitled to. Lighthouse and its partner Svenske Dagbladet (SvD) managed to obtain previously unpublished data about one of the agency’s machine learning models that allowed us to test whether it discriminates against certain groups. We published the underlying data and analysis on Github.

We found that:

– Women are especially disadvantaged by the model. Despite random sampling showing that they do not make more mistakes on their benefit applications than men, they are more than 1.5 times more likely to be selected for investigation by the model.

– Women, people with a foreign background, people who make below the median Swedish income and people without a university degree are overrepresented in the model’s predictions

– Women, people with a foreign background, people who make below the median Swedish income and people without a university degree who have not made mistakes on their benefit applications are wrongly flagged at higher rates than opposite groups.

– A fairness process later implemented by the Swedish Social Insurance Agency to ensure equal treatment of welfare recipients is self-serving and allows for broad discrimination.

– The Swedish Social Insurance Agency’s methodology for estimating fraud amongst benefit applicants is flawed and unsound.

HOW WE ACQUIRED THE DATA

Sweden consistently tops global transparency indexes and it has one of the world’s oldest freedom-of-information laws. We have sent freedom-of-information requests in nine countries and variously received runnable machine learning models, source code and comprehensive technical documentation. The Swedish Social Insurance Agency (SIA) has, by a large margin, been the least transparent.

In October of 2021, we sent a freedom-of-information request to the SIA regarding their use of risk-scoring algorithms. The request was denied. Over the next three years, we continually sent freedom-of-information requests and press questions about these systems. The refusals were relentless. The agency refused to disclose whether its models were trained on random samples or even how many people had been flagged by a model at all, claiming that this information could allow fraudsters to game the system.

The refusals were so extreme that at one point we decided to conduct an experiment and asked for information that we knew the agency had published in its annual reports. The agency refused to provide the information, claiming that it was confidential.

In one email chain, a high level official at the agency wrote, referring to one of our reporters, “let’s hope we are done with him!” after seemingly forgetting to remove the reporter from CC.

We saw an opportunity when we discovered a 2018 report in which the ISF, an independent supervisory agency of the Swedish Social Insurance Agency, investigated the agency’s use of risk-scoring algorithms. In its report, the ISF concluded that the agency’s model “in its current design does not pass for equal treatment.” The social security agency rejected the ISF’s conclusions and questioned the validity of their analysis.

We used FOI laws to request the underlying data for the report from the ISF. The supervisory agency disclosed it, despite the SIA having refused access to the exact same dataset.

The dataset delivered to Lighthouse pertains to the model used to score applicants for Sweden’s temporary parental allowance benefit scheme. The scheme pays compensation to parents who take time off work to care for sick children.

The dataset contains 6,129 people that were selected for investigation in 2017 and the outcome of that investigation: whether mistakes were or were not found in the benefit recipients’ application. Of the 6,129 cases, 1,047 were randomly selected and 5,082 were selected by the machine learning model.

We received, in essence, five versions of the dataset, each broken down by one of the following demographic characteristics: gender; born abroad; income; education; foreign background. The Swedish Statistics Bureau defines foreign background as either having been born abroad or having both parents having been born abroad. The dataset is pseudo-anonymized and it is therefore impossible to merge different demographic characteristics. You can find the complete dataset we analyzed on our Github.

This is the extent of the (technical) materials that Lighthouse has access to. The SIA refused to disclose code or the input variables for the model. These materials would have helped us to understand which characteristics of the benefit applicant the model uses to make its predictions. The agency has also refused to disclose more recent fairness or anti-discrimination evaluations of the model.

This is despite the supervisory authority, which provided us the above data, publishing earlier aggregate fairness results to the public. The SIA also declined to explain how disclosing fairness results for demographic characteristics outside of welfare recipients’ control would allow them to evade investigation.

FAIRNESS: TECHNICAL DEFINITIONS

In 2016, US investigative newsroom ProPublica published Machine Bias, an investigation into COMPAS, a risk assessment algorithm deployed in the US court system. ProPublica found that COMPAS was biassed because it was more likely to wrongly label black defendants as future criminals than white defendants. In response, Northpointe, the company that developed COMPAS, rejected ProPublica’s results and its metric for measuring bias.

The publication of Machine Bias sparked intense debate within the academic community about how to determine whether a machine learning algorithm is biassed against certain groups. Academics enumerated dozens of statistical definitions of fairness, some of which are incompatible with one another.

The appropriateness of each measure of fairness depends on context, and each definition comes with its own tradeoffs. Governments often prefer definitions that focus on the reliability of a model’s predictions, whereas civil rights groups will often favour definitions that focus on groups that are disproportionately impacted by investigations.

Fairness is also a broader discussion than statistical measures of equal treatment. The deployment of predictive algorithms in public services — especially those that can have punitive consequences for people — raises larger questions about due process and whether it is fair to judge people not on their own behaviour, but the past behaviour of people who share demographic characteristics.

Most common fairness measures compare a model’s accuracy across different groups. There are different ways to look at accuracy. One could look at false positives (i.e. people wrongly flagged for investigation) or false negatives (i.e. people wrongly not flagged for investigation). In practice, most mathematical fairness definitions mix and match different metrics. The table below outlines some key terminology and metrics that are used to calculate different fairness definitions.

For the purposes of this methodology, we use the word ‘mistake’ to indicate a mistake made by the benefit applicant on their application. The dataset we received does not indicate whether the mistake was unintentional or deliberate fraud. Nonetheless, the agency collapses these two categories and the applicants with the highest risk scores are automatically flagged for ‘control investigations’ where there is a suspicion of intent. Distinguishing between intentional mistakes and fraud is messy. We reveal major flaws in how the agency defines fraud below.

Conversely, we use the word ‘error’ to inculcate an incorrect prediction by the model.

Below, we test the data we received against six different fairness definitions. All of them show significant — at times extreme — differences in the ways that the model treats different groups of people.

RESULTS

1. Demographic Parity: The model selects women, people with foreign background, people without a university degree and people who earn below the median income at higher rates.

The first definition we tested — demographic parity — checks whether the model disproportionately flags certain demographic groups for investigation. It compares a group’s proportion within the welfare applicant population to its proportion in the people flagged as high risk by the model. Unlike the definitions we test below, statistical parity does not take into account whether the people selected by the model are actually found to have made a mistake.

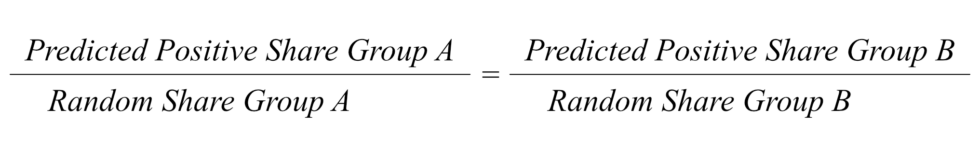
When we tested the data for demographic parity, we saw significant differences between demographic groups.

– Women are more than 1.5 times more likely to be selected by the algorithm than men.

– People with a foreign background are close to 2.5 times more likely to be selected than a person with a Swedish background.

– People without a university degree are more than 3.31 times more likely to be selected than people with a university degree.

– People who earn less than the median income are 2.97 times more likely to be selected than people who earn above the median income.

2. False Positive Error Rate: The model is more likely to wrongly flag women, people with a foreign background, people without a university degree and people who earn below the median income.

False positive error rate looks at whether an algorithm is more likely to wrongly label innocent people from a group as high risk. In other words, the proportion of women who have not made a mistake being wrongly labelled as high risk should be equal to the proportion of men who have not made a mistake being wrongly labelled high risk.

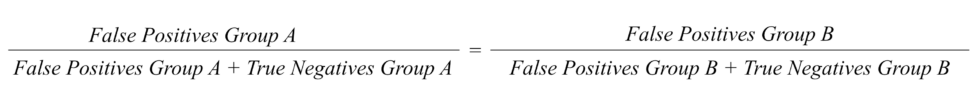
Because the number of investigations (≈6,000) is small compared to the total number of welfare applications (977,730), the share of true and false positives is small.

We saw large disparities between groups when we tested for false positive error rate balance. In particular:

– A woman who has not committed any mistakes is more than 1.7 times more likely to be wrongly flagged than a man who has not committed any mistakes.

– A person of foreign background who has not committed any mistakes is 2.4 times more likely to be wrongly flagged than a person with a Swedish background who has not committed any mistakes.

– A person without a university degree who has not committed any mistakes is more than 3 times more likely to be wrongly flagged than someone with a university degree who has not committed any mistakes.

– A person who earns below the median income who has not committed any mistakes is more than 3 times more likely to be wrongly flagged than someone who earns above the median income who has not committed any mistakes.

We also tested the inverse of false positive rate: false negative rate. We found that the model was more likely to incorrectly not flag men, people with a Swedish background, with a university degree and who make above the median income who did make a mistake on their application

3. Predictive Parity: The model is less precise for women, people with a Swedish background, people with a university degree and people who make above the median income.

Predictive parity compares a form of accuracy — precision — across groups. It looks at the ratio between correct positive predictions (true positives) and all predictions (predicted positives). In other words, it checks whether the model correctly flags people for potential mistakes.

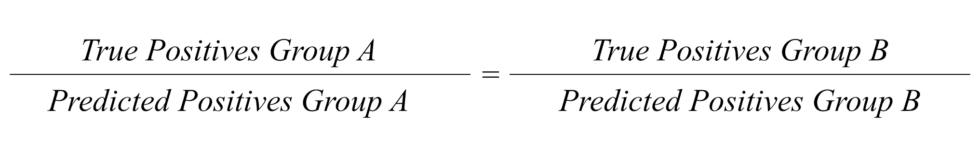
Predictive parity focuses on the reliability of a model’s predictions. It is often favoured by government’s deploying risk assessments because it focuses on correctly identifying as many flagged people as possible, even if that increases the overall number of false positives or false positive disparities between groups.

When we tested predictive parity, we also saw statistically significant differences between groups, with women, people with a Swedish background, with a university degree, or who earn above the median income disadvantaged. It’s important to note that under many conditions predictive parity is incompatible with some of the other definitions we test, like false positive error rate.

Our analysis found:

– The model is 1.08 times more precise for men than women.

– The model is 1.20 times more precise for people of a foreign background than people with a Swedish background.

– The model is 1.19 times more precise for people without a university degree than people with a university degree.

– The model is 1.09 times more precise for people who earn below the median income than people who earn above the median income.

4. Equal Burden: Women and people with a foreign background are unfairly burdened

Academics have also proposed fairness definitions that move away from comparing different forms of accuracy across groups.

One approach proposed in a paper authored by Petersen et al. from the Danish Technical University checks whether “burden” (in this case, being put under investigation) is distributed fairly across different groups. In order to do this, it compares the “ground truth” values (i.e. the rate at which a group makes mistakes in a representative, random sample) to the model’s predictions.

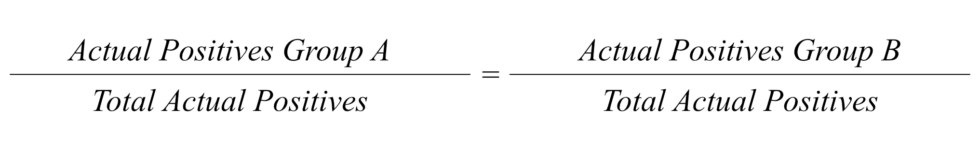
This definition is met when the share of a group in a representative, random sample of people who made a mistake is equal to a group’s share in people flagged by the model. The idea is that a model’s predictions should fairly reflect the real world distribution of people who make mistakes on their applications.

In its report, the supervisory authority of the Social Insurance Agency uses a similar definition of fairness, which the agency later questioned. It compares a group’s share of mistakes detected in a random sample to their share in mistakes detected by the model.

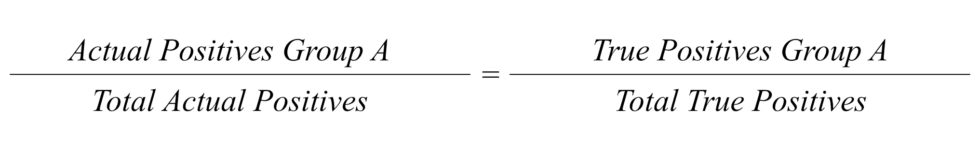
According to both definitions, the model does not distribute burden fairly. Women, people with a foreign background, people without a university degree and people who earn below the median income are unfairly burdened. These groups are overrepresented in the model’s predictions and true positives compared to the number of mistakes they make in the real world.

SOCIAL INSURANCE AGENCY'S FAIRNESS PROCESS

After the Supervisory Authority published the results of its fairness evaluation, the Social Insurance Agency published a public reply where it rejected their findings. The SIA argued that it is not clear whether its supervisory authority’s fairness tests are “accepted ways of testing equal treatment.”

A document we obtained using freedom-of-information laws, however, describes a new fairness process that the SIA designed to ensure equal treatment of protected groups. It is unclear whether the SIA has ever implemented it in practice. The agency has refused to provide any results related to its fairness process, so we ran the data we obtained instead

The agency’s fairness process has two steps that each apply a different fairness definition.

Step 1. A version of statistical / demographic parity. For each group, the SIA compares its percentage in the random sample and its percentage in the algorithmic sample. If their percentage has doubled or halved, it fails the test. If their percentage increases or decreases by more than 30 percentage points, it also fails this test.

If, for the group in question, the model passes this test, the agency skips Step 2. and concludes no adjustments are needed for that group. If the model fails this test for a particular group, the SIA moves to step 2.

Step 2. A version of predictive parity. For each group that failed Step 1. The agency compares its share in the risk-based sample to its share in true positives detected by the model. If there is a difference of more than 10 percentage points, the test is failed.

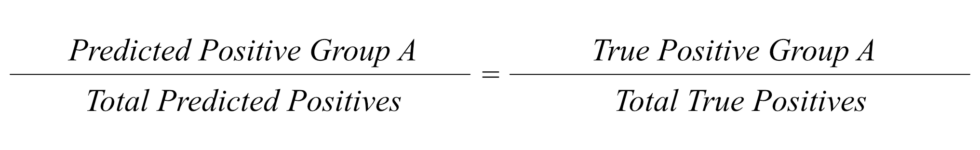
If, for the group in question, the model passes step 2 then the agency concludes no adjustments are needed. If it fails step 2, the agency moves to step 3.

Step 3. If Step 2. is also failed for a particular group, the values unit of the agency’s legal department examines the results and determines whether the model can be deployed regardless. The SIA has refused to disclose how often this happens in practice.

We ran the data we received through steps 1 and 2 of the SIA’s fairness process. While according to the agency’s process only groups that fail step 1 have to be checked against step 2, we tested all groups against both.

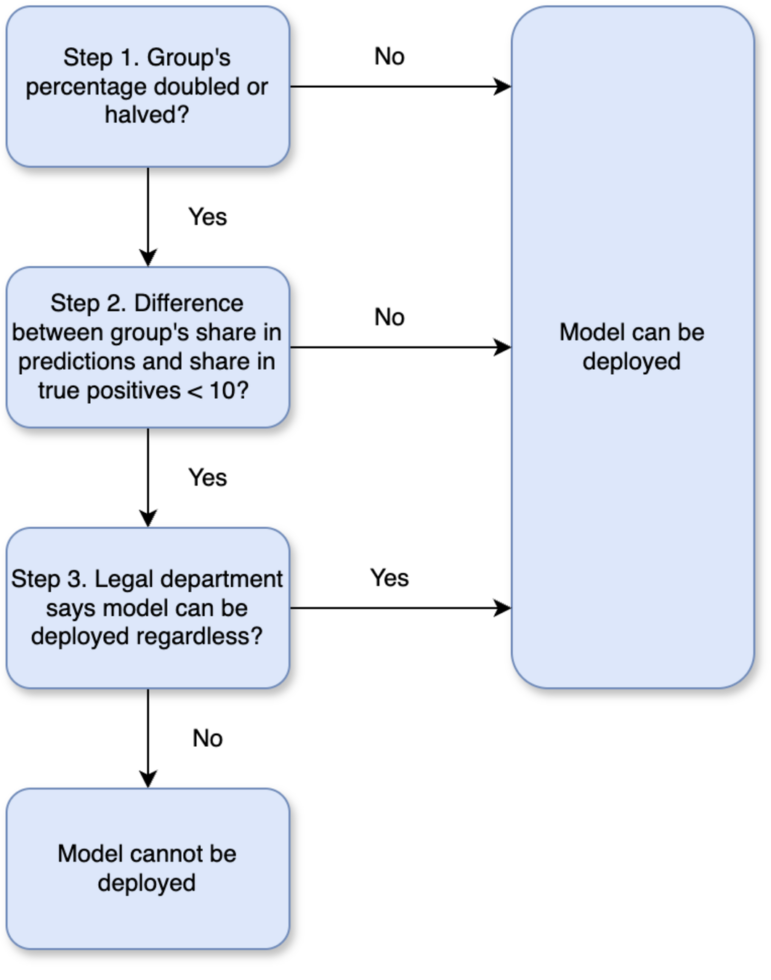
We ran the data we received through steps 1 and 2 of the SIA’s fairness process. While according to the agency’s process only groups that fail step 1 have to be checked against step 2, we tested all groups against both.

Nearly all groups passed the first step of the SIA’s fairness procedure with the exception of higher education, which failed because its proportion halved. All groups passed the second step of the agency’s fairness procedure. The model would therefore be considered acceptable to be deployed.

Analysis of Social Insurance Agency’s Fairness Process

The data we received passes the SIA’s fairness procedure and, if we follow it, the model would have not had to be adjusted. We however see a number of flaws in the agency’s process.

The first flaw is that the threshold for the first step is so high that it enables large differences in over and underrepresentation. In fact, the threshold is so large that it would allow for the model to select nearly four times as many women as men for investigations.

The second flaw is that if the model passes step 1 for a group, then that group does not have to be tested against step 2. In practice, this means that there can be substantial differences in the rates at which different groups are flagged and the SIA will not have to check whether that overrepresentation is justified. Furthermore, groups could be selected at equal rates (step 1) but have large disparities when it comes to model performance (step 2).

The third flaw is that the SIA does not check for intersectional bias. If women and people of a migration background are disadvantaged, then women with a migration background may be especially disadvantaged. The agency’s tests would not pick up on this bias.

The final flaw is that the SIA does not compare these metrics between groups, as is often done in the academic literature. When we put the standard definition of predictive parity (which does compare between groups) beside the agency’s version of predictive parity (Step 2 in their process), we see much larger disparities.

AGENCY'S FRAUD ESTIMATES

The Social Insurance Agency’s most common argument for refusing to disclose information was that disclosure would hinder its fraud prevention efforts. It has also pointed to temporary parental assistance, the benefit covered by the model we investigated, as being one of the most problematic schemes when it comes to fraud.

The Social Insurance Agency estimates that each year it wrongly pays out SEK 1.3 billion (€113 million) to parents who apply for temporary parental assistance. It further claims that SEK 800 million (€69 million), or more than half of what is wrongly paid, is lost because of parents who intentionally defraud the agency.

This projection of extensive fraud has been published by the media, highlighted in annual reports and reported to Swedish authorities. It has driven public discourse around Sweden’s social security system and enabled budgets and legislation that have granted the authority new powers in the name of fighting fraud. This includes its fraud prediction models. It is also one of the primary justifications for the secrecy surrounding the agency’s use of machine learning to detect fraud.

We wanted to investigate how the agency arrives at its fraud estimates. The agency refused to answer our requests for comprehensive statistics relating to its fraud investigations. Some of the data it refused were nonetheless available in its own public reports. The data we found cast serious doubts on the agency’s claim that there is widespread intentional cheating.

Data we obtained both from the agency and the Swedish criminal justice system show that very few cases where the Social Insurance Agency allege fraud reach the courts. It also shows that courts rarely determine that a defendant has intentionally committed fraud.

In 2022, the investigations department of the Social Insurance Agency investigated 5,520 cases of suspected fraud in temporary parental assistance. The agency referred 1,686 — or roughly 30.5 percent — of these cases to the police. The following year, prosecutors reported the outcome in 1,054 cases: 166 convictions and 83 plea bargains.

The Swedish Social Insurance Agency’s estimates of fraud are not actually based on investigations that have determined intentional cheating. Instead, it extrapolates an estimate based on a random sample of parents who applied for temporary parental assistance. The agency’s case workers checked applications in the sample to determine which days in each application were paid out incorrectly. They did not establish whether the mistakes made by the parents were intentional or unintentional; investigations with suspicion of intent are handled by the agency’s investigation department.

Case workers found that 20.2 percent of applications in the random sample contained at least one day incorrectly paid out. The agency chose to label all applications that contained two or more incorrect days as fraud, despite no investigation determining that the mistakes were intentional.

Our analysis found that this threshold carries large implications for the agency’s fraud estimates. With the agency’s two-day threshold, nearly a quarter of applications with mistakes are estimated to be sent in intentionally. With a four-day threshold, that number plummets to just over 6 percent.

In response to a set of questions from Lighthouse and SvD, the agency refused to justify why it chose this two-day cutoff to define fraud, writing that the release of this information would “make it easier for those who want to commit fraud.”

AGENCY'S RESPONSE

Lighthouse and SvD have exchanged hundreds of emails with the Social Insurance Agency over the course of this investigation. While the agency previously rejected the findings of its supervisory authority, it did not refute the findings or design of our analysis. Instead, it argued that certain demographic groups being wrongly selected for investigation at higher rates than others is not a disadvantage because a human investigator always makes the final decision.

The Social Insurance Agency refused to explain why it created an equal treatment procedure if it does not consider an investigation to be a disadvantage, simply responding it chose to do so because it was “appropriate.” The agency did confirm in an interview that it uses the equal treatment procedure, but refused to disclose how many times it has been used in practice. It declined to share the results of its equal treatment procedure, arguing that disclosure could aid fraudsters in gaming the system.

In response to a set of questions submitted by Lighthouse and Svenska Dagbladet, the Social Insurance Agency defended its use of machine learning to predict fraud, arguing that its models are more accurate than random selection. It also stated that the use of risk assessments was proportional and that it “is not something that the Social Insurance Agency has invented, but a standard way of working.”

The agency pointed to machine learning models as an essential part of its mandate to fight fraud.

“In society in general, risk-based controls are used today by public actors, banking, insurance and retail,” the agency wrote. “We have a mission to stop incorrect payments and fraud and to ensure that those who are entitled to benefits receive them.”

LIMITATIONS

In our previous investigations in the Netherlands and France, we were able to obtain runnable code and model files that allowed us to interrogate fairness implications across the algorithmic lifecycle. The limitation of these investigations was that we were never able to obtain outcome data (ie. whether a person flagged for investigation actually committed fraud).

This investigation comes with the opposite limitation: while we now have outcome data, the model itself is a complete black box. We therefore do not understand how or why certain types of bias have manifested in the model.

Another limitation of this investigation is the data we analysed is from 2017. It is possible that the discriminatory patterns we outline in this methodology have changed. We asked the SIA for the same data they supplied the ISF for more recent years, but they refused, arguing — without evidence — that this would allow people to circumvent their controls. The agency also refused to provide the results of its own fairness process.

Finally, we were unable to merge the data we had across different characteristics. This means that we could not analyse bias at the intersection of different traits (e.g. gender and foreign background).

APPENDIX I. CONFUSION MATRICES

The data we received allows us to construct confusion matrices for each of the protected classes. See the confusion matrices for gender below. Note that the number of true positives and false positives are quite low. This is because the number of people selected by the model (5,082) is quite small in comparison to the number of people who apply for temporary parental benefits (~977,730).

To calculate the confusion matrices for various demographic groups, we assumed that the model was deployed against the 977,730 welfare recipients that applied in 2017. We estimated the share of demographic groups within the beneficiary population by multiplying a group’s share in the random sample by 977,730 (group total). For example, 43.94 percent of the population in the random sample is male, meaning that the group total for men is 977,730 x 43.94 = 429,614.

With this number in hand, we could calculate the share of TP and TN by dividing the number of correctly and wrongly flagged individuals in the Algorithmic Sample by the group total. Finding the share of predicted positives and negatives worked much in the same way: we simply divided the number of people in a given group by the group total. To calculate the share Actual Positives and Actual Negatives for each group, we looked at the share of mistakes found and mistakes not found in the Random Sample. Now, it was simply an exercise of filling in the blanks. E.g., FN is simply Actual Positives – TP.

APPENDIX II. BOOTSTRAPPING

For all definitions, we bootstrapped p-values to bulletproof our findings. Conventionally, estimating uncertainty and significance levels relies on strong assumptions about the distribution of e.g., false positives for the groups we are comparing. To ensure that the observed differences are in fact statistically significant we instead rely on bootstrapped p-values. In this procedure, we resampled the available data 10,000 times with replacement and, for each sample, compared mean differences for each of the definitions enumerated above. Our null hypothesis is that the difference is equal to zero. The reported p-values are the share of the samples where the mean difference is directionally opposite to the mean difference in the raw data.